07 Calculus: Multivariate
Գյումրի, լուսանկարի հղումը, Հեղինակ՝ Naren Hakobyan
📚 Նյութը
YouTube links in this section were auto-extracted. If you spot a mistake, please let me know!
Դասախոսություն
Գործնական
🏡 Տնային
- ❗❗❗ DON’T CHECK THE SOLUTIONS BEFORE TRYING TO DO THE HOMEWORK BY YOURSELF❗❗❗
- Please don’t hesitate to ask questions, never forget about the 🍊karalyok🍊 principle!
- The harder the problem is, the more 🧀cheeses🧀 it has.
- Problems with 🎁 are just extra bonuses. It would be good to try to solve them, but also it’s not the highest priority task.
- If the problem involve many boring calculations, feel free to skip them - important part is understanding the concepts.
- Submit your solutions here (even if it’s unfinished)
01 Gradient Descent Algorithm
Consider the function \(f(x_1, x_2) = x_1^2 + 2x_2^2 + x_1 x_2 + 4x_1 - 2x_2 + 5\).
We want to find the minimum. We could do it analytically, it’s just a quadratic function, but quite soon we’ll start to work with function for which we can’t just find the optimum with pen and paper. So let’s use an iterative algorithm.
- Open up VS code, or you’re favorite IDE.
- Pick a random starting point.
- In what direction should you move so that the function value decreases in the fastest way?
- Move in that direction (you may consider first multiplying that direction by some small value, let’s say 0.1, that’s the so called \(\alpha\)’learning rate’ / ‘step size’, which we’ll learn about later, but it basically controls how big steps you take. Too big step size -> you may overshoot the optimum value and diverge, too small, you may take too long time to converge, but often “Let it be late, let it be almond” principle holds)
- Keep on iterating like that. Can you come up with a stopping criteria? (e. g. if improvement / change smaller then x let’s just stop the algorithm)
- Plot and print interesting staff, e. g. function value vs iteration number
- Play around with \(\alpha\) and the starting point to see how it affects convergence.
02 Boat in Sevan
Սևանա լճի \((x, y)\) կոորդինատներով կետում ջրի խորությունը
\[ f(x, y) = xy^2 - 6x^2 - 3y^2 \]
մետր է։ \((5, 3)\) կետում գտնվող «Նորատուս» առագաստանավի նավապետը ցանկանում է շարժվել դեպի մի այնպիսի կետ, որում ջուրն ավելի խոր է։ Նրա առաջին օգնականն առաջարկում է նավարկել դեպի հյուսիս, իսկ երկրորդը՝ դեպի հարավ։ Օգնականներից որի՞ խորհուրդը պետք է լսի նավապետը։
Setup. Depth at \((x, y)\) is \(f(x, y) = xy^2 - 6x^2 - 3y^2\). The captain stands at \((5, 3)\) and must decide between north (increasing \(y\), direction \((0, 1)\)) and south (decreasing \(y\), direction \((0, -1)\)).
The instantaneous rate of change of \(f\) when moving in a unit direction \(\mathbf{u}\) is the directional derivative:
\[D_{\mathbf{u}} f(\mathbf{x}) = \nabla f(\mathbf{x}) \cdot \mathbf{u}\]
So we just need \(\partial f / \partial y\) at \((5, 3)\) — that’s exactly the rate of change in the north direction.
Compute the gradient.
\[\frac{\partial f}{\partial x} = y^2 - 12x, \qquad \frac{\partial f}{\partial y} = 2xy - 6y\]
At \((5, 3)\):
\[\frac{\partial f}{\partial y}\bigg|_{(5,3)} = 2 \cdot 5 \cdot 3 - 6 \cdot 3 = 30 - 18 = 12 > 0\]
Decision. Moving north (in direction \((0, 1)\)) gives directional derivative \(+12\) — depth increases at rate \(12\) m per unit of distance. Moving south gives \(-12\) — depth decreases. So the captain should listen to the first assistant and head north.
Sanity check on the full gradient. \(\nabla f(5, 3) = (9 - 60, \; 12) = (-51, 12)\). So north isn’t actually the optimal direction — the steepest-ascent direction is \((-51, 12)/\|(-51, 12)\|\), roughly west-northwest. But between only the two options offered (north vs. south), north wins.
ML connection. This is exactly how gradient ascent works: project the gradient onto the available “moves” and pick the one with the highest dot product. In gradient descent we’d flip the sign — head in the direction with the most negative directional derivative.
03 Topless box
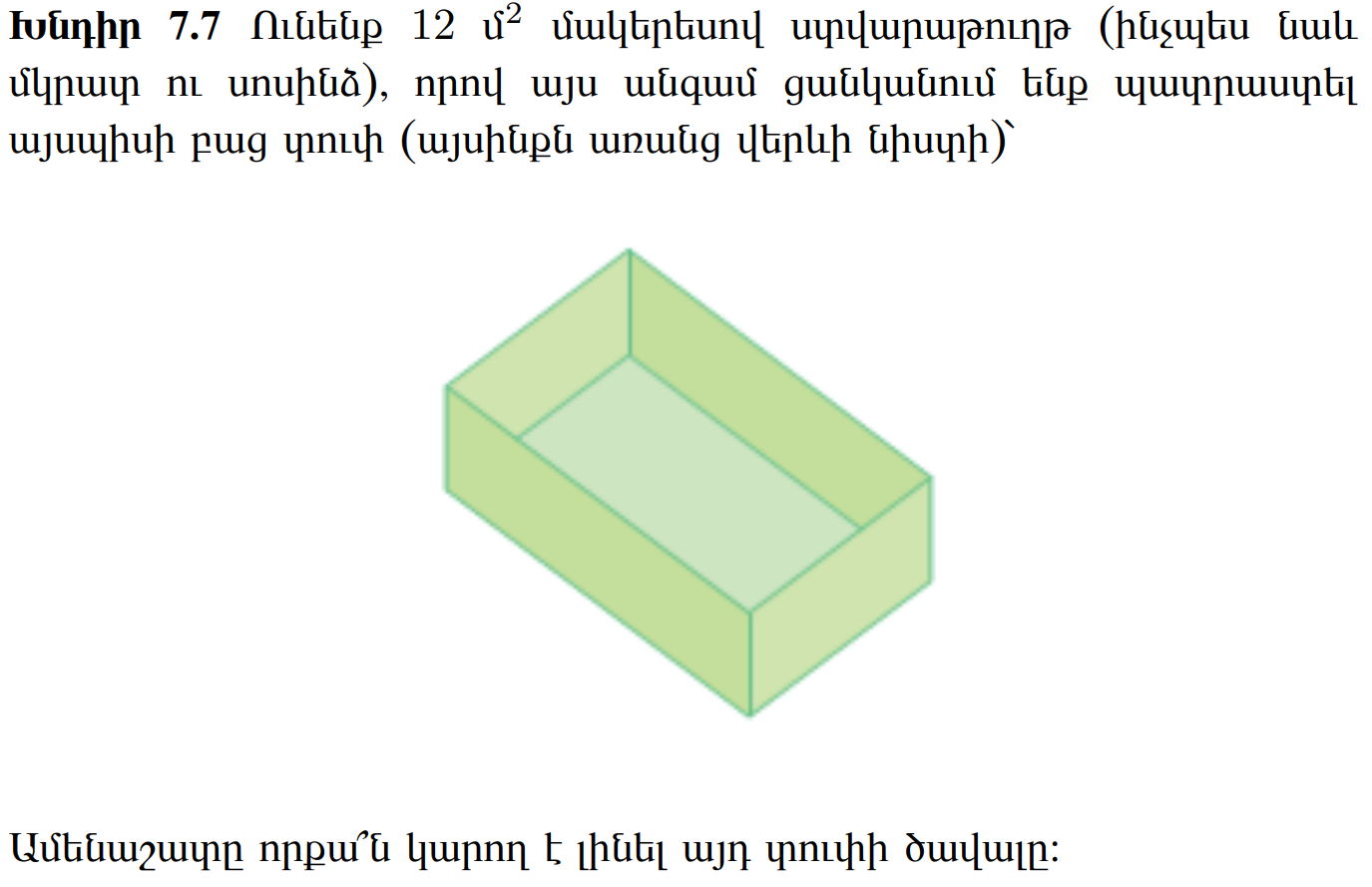
Hint: You may want to first do this exercise. ### 04 Smooth Functions and Gradient Properties {data-difficulty=“3”}
A function \(f: \mathbb{R}^n \to \mathbb{R}\) is called smooth (or \(C^\infty\)) if it has continuous partial derivatives of all orders. In practice, we often work with \(C^1\) functions (continuously differentiable) or \(C^2\) functions (twice continuously differentiable).
Consider the bivariate function \(f : \mathbb{R}^2 \to \mathbb{R}\), \((x_1, x_2) \mapsto x_1^2 + 0.5x_2^2 + x_1x_2\).
- Show that \(f\) is smooth (continuously differentiable).
- Find the direction of greatest increase of \(f\) at \(\mathbf{x} = (1, 1)\).
- Find the direction of greatest decrease of \(f\) at \(\mathbf{x} = (1, 1)\).
- Find a direction in which \(f\) does not instantly change at \(\mathbf{x} = (1, 1)\).
- Assume there exists a differentiable parametrization of a curve \(\tilde{\mathbf{x}} : \mathbb{R} \to \mathbb{R}^2\), \(t \mapsto \tilde{\mathbf{x}}(t)\) such that \(\forall t \in \mathbb{R} : f(\tilde{\mathbf{x}}(t)) = f(1,1)\). Show that at each point of the curve \(\tilde{\mathbf{x}}\) the tangent vector \(\frac{\partial \tilde{\mathbf{x}}}{\partial t}\) is perpendicular to \(\nabla f(\tilde{\mathbf{x}})\).
- Interpret parts (d) and (e) geometrically.
\(f(x_1, x_2) = x_1^2 + 0.5 x_2^2 + x_1 x_2\).
1. Smoothness. \(f\) is a polynomial. All partial derivatives of all orders exist and are continuous everywhere — every derivative is itself a polynomial. So \(f \in C^\infty(\mathbb{R}^2)\), in particular \(C^1\). ✓
2. Direction of greatest increase at \((1, 1)\).
The gradient:
\[\nabla f(x_1, x_2) = \begin{pmatrix} 2x_1 + x_2 \\ x_2 + x_1 \end{pmatrix}\]
At \((1, 1)\): \(\nabla f(1, 1) = (3, 2)\).
The direction of greatest rate of increase is the unit gradient:
\[\mathbf{u}_{\uparrow} = \frac{\nabla f(1,1)}{\|\nabla f(1,1)\|} = \frac{1}{\sqrt{13}}\begin{pmatrix} 3 \\ 2 \end{pmatrix}\]
Why? For any unit vector \(\mathbf{u}\), \(D_{\mathbf{u}} f = \nabla f \cdot \mathbf{u} = \|\nabla f\|\cos\theta\), maximized when \(\theta = 0\) — i.e. \(\mathbf{u}\) aligned with \(\nabla f\).
3. Direction of greatest decrease at \((1, 1)\).
By the same logic, minimized when \(\theta = \pi\) — opposite to the gradient:
\[\mathbf{u}_{\downarrow} = -\frac{\nabla f(1,1)}{\|\nabla f(1,1)\|} = \frac{1}{\sqrt{13}}\begin{pmatrix} -3 \\ -2 \end{pmatrix}\]
This is exactly the direction gradient descent moves — “follow \(-\nabla f\).”
4. Direction of zero instantaneous change.
We need \(\nabla f(1, 1) \cdot \mathbf{u} = 0\), i.e. \(\mathbf{u}\) perpendicular to \((3, 2)\). Two unit choices:
\[\mathbf{u}_{\perp} = \pm \frac{1}{\sqrt{13}}\begin{pmatrix} -2 \\ 3 \end{pmatrix}\]
5. Tangent to a level curve is orthogonal to the gradient.
Suppose \(f(\tilde{\mathbf{x}}(t)) = c\) (constant) for all \(t\). Differentiate both sides with respect to \(t\) using the chain rule:
\[\frac{d}{dt} f(\tilde{\mathbf{x}}(t)) = \nabla f(\tilde{\mathbf{x}}(t)) \cdot \frac{d\tilde{\mathbf{x}}}{dt} = 0\]
Since the right-hand side is \(0\) for all \(t\), the tangent vector \(\frac{d\tilde{\mathbf{x}}}{dt}\) is perpendicular to \(\nabla f\) at every point of the curve. ✓
6. Geometric interpretation.
Part (4) found a direction where \(f\) doesn’t change instantaneously at \((1, 1)\). Part (5) showed that any curve along which \(f\) stays constant has its tangent perpendicular to \(\nabla f\). Together: the gradient is perpendicular to the level curves of \(f\).
This is one of the most important geometric facts in multivariate calculus:
- Level curves of \(f\) are the contour lines \(\{f = c\}\) — like elevation lines on a topographic map.
- The gradient \(\nabla f\) points uphill, perpendicular to those contour lines, in the direction of steepest ascent.
- The directions you found in part (4) are tangents to the level curve passing through \((1, 1)\).
ML connection. Gradient descent moves perpendicular to the contour lines of the loss surface. This is why the trajectory zig-zags through long narrow valleys: each step is perpendicular to the current contour, but the contours of an ill-conditioned quadratic are stretched ellipses, so the perpendiculars don’t point at the minimum. Methods like Newton’s method and momentum fix this by not going strictly perpendicular to contours.
05 Contour Plots, Hessians, and Convexity
Contour plots (or level curves) visualize multivariate functions by showing curves where \(f(x_1, x_2) = c\) for various constants \(c\). They’re essential for understanding the shape of loss landscapes in machine learning.
Let \(f : \mathbb{R}^2 \to \mathbb{R}\), \((x_1, x_2) \mapsto -\cos(x_1^2 + x_2^2 + x_1x_2)\).
- Create a contour plot of \(f\) in the range \([-2,2] \times [-2,2]\) with R.
- Compute \(\nabla f\).
- Compute \(\nabla^2 f\) (the Hessian matrix).
Now, define the restriction of \(f\) to \(S_r = \{(x_1, x_2) \in \mathbb{R}^2 \mid x_1^2 + x_2^2 + x_1x_2 < r\}\) with \(r \in \mathbb{R}, r > 0\), i.e., \(f|_{S_r} : S_r \to \mathbb{R}, (x_1, x_2) \mapsto f(x_1, x_2)\).
- Show that \(f|_{S_r}\) with \(r = \pi/4\) is convex.
- Find the local minimum \(\mathbf{x}^*\) of \(f|_{S_r}\).
- Is \(\mathbf{x}^*\) a global minimum of \(f\)?
Let \(u(x_1, x_2) = x_1^2 + x_2^2 + x_1 x_2\) so \(f = -\cos(u)\). We’ll lean on the chain rule a lot — it’s much cleaner than expanding everything.
1. Contour plot (R skipped — we’ll just describe it).
The level sets \(\{f = c\}\) are determined by \(u(x_1, x_2) = \text{const}\). Since \(u\) is a positive-definite quadratic form (its matrix \(\bigl(\begin{smallmatrix} 1 & 1/2 \\ 1/2 & 1 \end{smallmatrix}\bigr)\) has eigenvalues \(\tfrac{3}{2}, \tfrac{1}{2}\), both positive), level sets of \(u\) are concentric ellipses centered at \((0, 0)\), with major axis along \((1, -1)\) and minor along \((1, 1)\). The contours of \(f = -\cos(u)\) are the same ellipses, but the function value oscillates as \(u\) grows: \(f = -1\) when \(u = 0, 2\pi, 4\pi, \ldots\) (deep blue rings) and \(f = +1\) when \(u = \pi, 3\pi, \ldots\) (red rings).
2. Gradient \(\nabla f\). By the chain rule, \(\nabla f = -\cos'(u) \cdot \nabla u = \sin(u) \nabla u\), where
\[\nabla u(x_1, x_2) = \begin{pmatrix} 2x_1 + x_2 \\ 2x_2 + x_1 \end{pmatrix}\]
So:
\[\nabla f(x_1, x_2) = \sin(x_1^2 + x_2^2 + x_1 x_2) \begin{pmatrix} 2x_1 + x_2 \\ 2x_2 + x_1 \end{pmatrix}\]
3. Hessian \(\nabla^2 f\). Differentiating \(\nabla f = \sin(u) \nabla u\) once more, by the product rule:
\[\nabla^2 f = \cos(u) \, (\nabla u)(\nabla u)^\top + \sin(u) \, \nabla^2 u\]
where \(\nabla^2 u = \bigl(\begin{smallmatrix} 2 & 1 \\ 1 & 2 \end{smallmatrix}\bigr)\) (constant) and \((\nabla u)(\nabla u)^\top\) is the rank-1 outer product:
\[(\nabla u)(\nabla u)^\top = \begin{pmatrix} (2x_1 + x_2)^2 & (2x_1+x_2)(2x_2+x_1) \\ (2x_1+x_2)(2x_2+x_1) & (2x_2 + x_1)^2 \end{pmatrix}\]
Combining:
\[\nabla^2 f = \cos(u)\,(\nabla u)(\nabla u)^\top + \sin(u)\begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix}\]
4. Convexity on \(S_{\pi/4}\).
We need \(\nabla^2 f(\mathbf{x}) \succeq 0\) for all \(\mathbf{x} \in S_{\pi/4}\), i.e. all \(\mathbf{x}\) with \(0 \le u(\mathbf{x}) < \pi/4\).
- \(\cos(u) > 0\) on \(u \in [0, \pi/4)\) since \(\pi/4 < \pi/2\). ✓
- \((\nabla u)(\nabla u)^\top\) is rank-1 with eigenvalues \(\|\nabla u\|^2\) and \(0\) — always positive semidefinite.
- \(\sin(u) > 0\) on \(u \in (0, \pi/4)\), and \(\nabla^2 u = \bigl(\begin{smallmatrix} 2 & 1 \\ 1 & 2 \end{smallmatrix}\bigr)\) has eigenvalues \(3, 1 > 0\) — positive definite.
- At \(u = 0\) (i.e. at \(\mathbf{x} = 0\)), \(\sin(u) = 0\) and \(\nabla u = 0\), so \(\nabla^2 f = 0\) there — at least PSD.
A positive linear combination (with nonnegative scalars \(\cos(u), \sin(u)\)) of a PSD matrix and a PD matrix is PSD; on the open interior \(u \in (0, \pi/4)\) it’s actually PD. So \(f|_{S_{\pi/4}}\) is convex (and strictly convex on the interior except at the single point \(\mathbf{x} = 0\)).
5. Local minimum.
On \(S_{\pi/4}\), \(f\) is convex, so any stationary point is a global min of the restriction. From part 2, \(\nabla f = 0\) requires either \(\sin(u) = 0\) or \(\nabla u = 0\).
- \(\sin(u) = 0\) on \(S_{\pi/4}\) only at \(u = 0\) (since \(u \in [0, \pi/4)\)).
- \(\nabla u = (2x_1 + x_2, x_1 + 2x_2) = 0\) has unique solution \((x_1, x_2) = (0, 0)\), which gives \(u = 0\) anyway.
So \(\mathbf{x}^* = (0, 0)\) with \(f(\mathbf{x}^*) = -\cos(0) = -1\).
6. Is \(\mathbf{x}^*\) a global minimum of the full \(f\)?
Yes, because \(f(\mathbf{x}) = -\cos(u(\mathbf{x})) \ge -1\) for all \(\mathbf{x} \in \mathbb{R}^2\) (since \(\cos \le 1\)), and \(f(0, 0) = -1\). So \(-1\) is the global min, achieved at \(\mathbf{x}^* = (0, 0)\).
But wait — it’s not the unique global min. \(f = -1\) whenever \(u = 2\pi k\) for any nonnegative integer \(k\), i.e. on every ellipse \(x_1^2 + x_2^2 + x_1 x_2 = 2\pi k\). So there are infinitely many points achieving the global minimum value, lying on a sequence of expanding ellipses around the origin.
ML connection. This is a great toy model of why convexity is local, not global, for many ML losses. Restricted to a small enough neighborhood, the loss surface looks convex and gradient descent finds the minimum cleanly. But globally, oscillating losses like this have many equivalent minima. Periodic activations and trigonometric reparameterizations (e.g. in Fourier features or sinusoidal positional encodings) inherit exactly this kind of geometry.
06 Taylor Expansion
Consider the bivariate function \(f : \mathbb{R}^2 \to \mathbb{R}, (x_1,x_2) \mapsto \exp(\pi \cdot x_1) - \sin(\pi \cdot x_2) + \pi \cdot x_1 \cdot x_2\).
- Compute the gradient of \(f\) for an arbitrary \(x\).
- Compute the Hessian of \(f\) for an arbitrary \(x\).
- State the first order taylor polynomial \(T_{1,a}(x)\) expanded around the point \(a = (0,1)\).
- State the second order taylor polynomial \(T_{2,a}(x)\) expanded around the point \(a = (0,1)\).
- Determine if \(T_{2,a}\) is a convex function.
\(f(x_1, x_2) = e^{\pi x_1} - \sin(\pi x_2) + \pi x_1 x_2\).
1. Gradient. Differentiate term by term:
\[\frac{\partial f}{\partial x_1} = \pi e^{\pi x_1} + \pi x_2, \qquad \frac{\partial f}{\partial x_2} = -\pi \cos(\pi x_2) + \pi x_1\]
\[\nabla f(x_1, x_2) = \pi \begin{pmatrix} e^{\pi x_1} + x_2 \\ -\cos(\pi x_2) + x_1 \end{pmatrix}\]
2. Hessian. Differentiate the gradient:
\[\frac{\partial^2 f}{\partial x_1^2} = \pi^2 e^{\pi x_1}, \quad \frac{\partial^2 f}{\partial x_2^2} = \pi^2 \sin(\pi x_2), \quad \frac{\partial^2 f}{\partial x_1 \partial x_2} = \pi\]
\[\nabla^2 f(x_1, x_2) = \begin{pmatrix} \pi^2 e^{\pi x_1} & \pi \\ \pi & \pi^2 \sin(\pi x_2) \end{pmatrix}\]
Evaluate at \(a = (0, 1)\):
- \(f(a) = e^0 - \sin(\pi) + \pi \cdot 0 \cdot 1 = 1 - 0 + 0 = 1\)
- \(\nabla f(a) = \pi \binom{1 + 1}{-\cos(\pi) + 0} = \pi \binom{2}{1}\) (using \(\cos\pi = -1\))
- \(\nabla^2 f(a) = \bigl(\begin{smallmatrix} \pi^2 & \pi \\ \pi & 0 \end{smallmatrix}\bigr)\) (using \(\sin\pi = 0\))
3. First-order Taylor polynomial around \(a\).
\[T_{1, a}(\mathbf{x}) = f(a) + \nabla f(a)^\top (\mathbf{x} - a) = 1 + \pi \begin{pmatrix} 2 \\ 1 \end{pmatrix}^\top \begin{pmatrix} x_1 \\ x_2 - 1 \end{pmatrix}\]
\[\boxed{\;T_{1, a}(\mathbf{x}) = 1 + 2\pi x_1 + \pi(x_2 - 1)\;}\]
4. Second-order Taylor polynomial around \(a\).
\[T_{2, a}(\mathbf{x}) = T_{1, a}(\mathbf{x}) + \tfrac{1}{2}(\mathbf{x} - a)^\top \nabla^2 f(a) (\mathbf{x} - a)\]
Compute the quadratic term with \(\mathbf{x} - a = (x_1, \, x_2 - 1)^\top\):
\[\tfrac{1}{2}(x_1, \; x_2 - 1) \begin{pmatrix} \pi^2 & \pi \\ \pi & 0 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 - 1 \end{pmatrix} = \tfrac{1}{2}\Big[\pi^2 x_1^2 + 2\pi x_1(x_2 - 1)\Big]\]
\[= \tfrac{\pi^2}{2} x_1^2 + \pi x_1 (x_2 - 1)\]
So:
\[\boxed{\;T_{2, a}(\mathbf{x}) = 1 + 2\pi x_1 + \pi(x_2 - 1) + \tfrac{\pi^2}{2} x_1^2 + \pi x_1 (x_2 - 1)\;}\]
5. Is \(T_{2, a}\) convex?
A quadratic is convex iff its Hessian is positive semidefinite. The Hessian of \(T_{2, a}\) is exactly \(\nabla^2 f(a) = \bigl(\begin{smallmatrix} \pi^2 & \pi \\ \pi & 0 \end{smallmatrix}\bigr)\).
Check via determinant + trace:
- \(\det = \pi^2 \cdot 0 - \pi \cdot \pi = -\pi^2 < 0\)
- Trace \(= \pi^2 > 0\)
Since \(\det < 0\), the eigenvalues have opposite signs (one positive, one negative). The Hessian is indefinite → \(T_{2, a}\) is neither convex nor concave. It’s a saddle-shaped quadratic.
Why the second-order Taylor can be non-convex. A common misconception is that the second-order Taylor expansion is always a “bowl.” That’s only true if the original function has a positive-definite Hessian at the expansion point. Here, \(f\) is not convex globally, and at the point \((0, 1)\) specifically, \(\sin(\pi \cdot 1) = 0\) kills the \(\partial^2 / \partial x_2^2\) entry, leaving the Hessian indefinite.
ML connection. Newton’s method approximates the loss locally by its second-order Taylor expansion and then jumps to that quadratic’s minimum. But if the local Hessian is indefinite (we’re near a saddle, not a basin), Newton’s method can step toward the saddle instead of away — a real failure mode in deep-learning loss landscapes, which are full of saddles. Modifications like trust-region and saddle-free Newton address this by replacing \(H\) with \(|H|\) (taking absolute values of eigenvalues).