Let \(f : [-1,2] \to \mathbb{R}, x \mapsto \exp(x^3 - 2x^2)\).
Compute \(f'(x)\).
Plot \(f\) and \(f'\) (you can use any graphing tool or software).
Find all possible candidates \(x^*\) for maxima and minima.
Hint: \(\exp\) is a strictly monotone function.
Compute \(f''(x)\).
Determine if the candidates are local maxima, minima or neither.
Find the global maximum and global minimum of \(f\) on \([-1,2]\).
Convexity
03 Convex Function Properties
Consider two convex functions \(f,g : \mathbb{R} \to \mathbb{R}\).
Show that \(f + g\) is convex.
Now, assume that \(g\) is additionally non-decreasing, i.e., \(g(y) \geq g(x)\) for all \(x \in \mathbb{R}\), for all \(y \in \mathbb{R}\) with \(y > x\). Show that \(g \circ f\) is convex.
04 Testing Convexity in ML Functions
Determine whether the following ML-related functions are convex, concave, or neither on the given intervals:
Mean Squared Error: \(L(w) = \frac{1}{2}(w - 3)^2\) on \(\mathbb{R}\)
ReLU Activation: \(\text{ReLU}(x) = \max(0, x)\) on \(\mathbb{R}\)
Sigmoid Function: \(\sigma(x) = \frac{1}{1 + e^{-x}}\) on \(\mathbb{R}\)
05 L2-Regularized Linear Regression
Consider the L2-regularized mean squared error loss function: \[R_\lambda(w) = \frac{1}{n}\sum_{i=1}^{n}(wx_i - y_i)^2 + \lambda w^2\]
where \(\{(x_i, y_i)\}_{i=1}^n\) are training data points, \(w\) is the model parameter, and \(\lambda > 0\) is the regularization parameter.
Find the optimum \(w^*\) and determine if it’s a minimum or maximum.
Is the function \(R_\lambda(w)\) convex? Justify your answer.
Is the minimizer unique? Explain why this is important for machine learning.
06 Logistic Loss and Its Properties
Context
The logistic loss is the foundation of logistic regression, one of the most important algorithms in machine learning for binary classification. Understanding its derivative is crucial for gradient-based optimization.
Consider the logistic loss function: \[\ell(z;y) = -y\log\sigma(z) - (1-y)\log(1-\sigma(z))\]
where \(\sigma(z) = \frac{1}{1+e^{-z}}\) is the sigmoid function, \(z\) is the logit (linear combination of features), and \(y \in \{0,1\}\) is the true binary label.
Task: Show that \(\frac{d}{dz}\ell(z;y) = \sigma(z) - y\).
Bonus: Check if the function \(g(z) = (y - \sigma(z))^2\) is convex with respect to \(z\).
07 Lipschitz Continuity & Gradient Clipping
Context: Lipschitz Continuity
A function \(f: \mathbb{R} \to \mathbb{R}\) is called L-Lipschitz continuous if there exists a constant \(L \geq 0\) such that: \[|f(x) - f(y)| \leq L|x - y|\] for all \(x, y\) in the domain. The smallest such constant \(L\) is called the Lipschitz constant.
This property is crucial in deep learning for gradient clipping, ensuring gradients don’t explode during training.
Consider the sigmoid function \(\sigma(z) = \frac{1}{1+e^{-z}}\).
Task: Prove that \(\sigma(z)\) is L-Lipschitz continuous and find the optimal (smallest possible) Lipschitz constant \(L\).
Taylor Series
08 Taylor Series Expansions
Find the Taylor series expansion around the given point for each function:
\(f(x) = e^x\) around \(x = 0\) (Maclaurin series)
---title: "05 Calculus: Extrema, Convexity, and Taylor Series"format: html: css: homework-styles.css---<script src="homework-scripts.js"></script>[լուսանկարի հղումը](https://unsplash.com/photos/man-in-black-suit-statue-twp2-YDQVn8), Գյումրի, Ֆրունզիկ, Հեղինակ՝ [Robert Levonyan](https://unsplash.com/@robertlevonyan)# 📚 Նյութը ToDo- [📚 Ամբողջական նյութը]()- [📺 Տեսագրությունը]()- [🎞️ Սլայդեր - ToDo](Lectures/L01_Vectors.pdf)- [🎞️ Սլայդեր - Geometry](Lectures/L02_Geometry_of_Vectors__Matrices.pdf)- [🛠️📺 Գործնականի տեսագրությունը](https://youtu.be/vectors_practical)- [🛠️🗂️ Գործնականի PDF-ը](Homeworks/hw_01_vectors.pdf)# 🏡 Տնային::: {.callout-note collapse="false"}1. ❗❗❗ DON'T CHECK THE SOLUTIONS BEFORE TRYING TO DO THE HOMEWORK BY YOURSELF❗❗❗2. Please don't hesitate to ask questions, never forget about the 🍊karalyok🍊 principle!3. The harder the problem is, the more 🧀cheeses🧀 it has.4. Problems with 🎁 are just extra bonuses. It would be good to try to solve them, but also it's not the highest priority task.5. If the problem involve many boring calculations, feel free to skip them - important part is understanding the concepts.6. Submit your solutions [here](https://forms.gle/CFEvNqFiTSsDLiFc6) (even if it's unfinished):::## Extrema ### 01 Box Problem {data-difficulty="2"}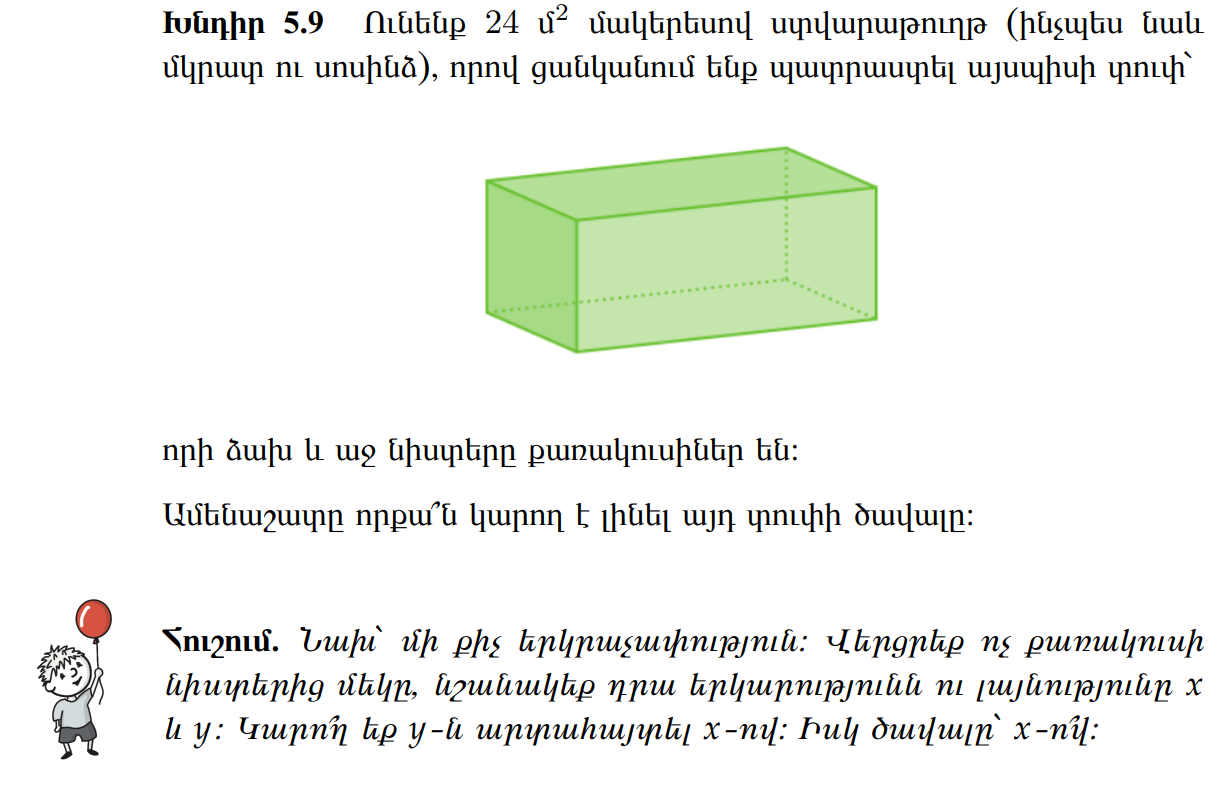[Video Solution in Armenian](https://www.youtube.com/watch?v=f2Bp77tiESg)### 02 Finding Local Extrema {data-difficulty="1"}Let $f : [-1,2] \to \mathbb{R}, x \mapsto \exp(x^3 - 2x^2)$.1. Compute $f'(x)$.2. Plot $f$ and $f'$ (you can use any graphing tool or software).3. Find all possible candidates $x^*$ for maxima and minima. *Hint: $\exp$ is a strictly monotone function.*4. Compute $f''(x)$.5. Determine if the candidates are local maxima, minima or neither.6. Find the global maximum and global minimum of $f$ on $[-1,2]$.::: {.content-visible when-profile="solution"}#### Solution {.solution-header}1. Using the chain rule: $f'(x) = \exp(x^3 - 2x^2) \cdot (3x^2 - 4x) = \exp(x^3 - 2x^2) \cdot x(3x - 4)$2. [Plot would show $f$ starting low, increasing to a peak, then decreasing and increasing again]3. Since $\exp(u) > 0$ for all $u$, we have $f'(x) = 0$ when $x(3x - 4) = 0$. Critical points: $x = 0$ and $x = \frac{4}{3}$ Also check endpoints: $x = -1$ and $x = 2$4. Using the product rule: $f''(x) = \exp(x^3 - 2x^2) \cdot (3x^2 - 4x)^2 + \exp(x^3 - 2x^2) \cdot (6x - 4)$ $f''(x) = \exp(x^3 - 2x^2) \cdot [(3x^2 - 4x)^2 + (6x - 4)]$5. Evaluating $f''$ at critical points: - $f''(0) = e^0 \cdot [0 + (-4)] = -4 < 0$ → local maximum - $f''(4/3) = \exp(\frac{64}{27} - \frac{32}{9}) \cdot [0 + 4] > 0$ → local minimum6. Evaluate at all candidates: - $f(-1) = e^{-1-2} = e^{-3}$ - $f(0) = e^0 = 1$ - $f(4/3) = \exp(\frac{64}{27} - \frac{32}{9}) = \exp(-\frac{32}{27}) < 1$ - $f(2) = e^{8-8} = e^0 = 1$ Global maximum: $1$ (at $x = 0$ and $x = 2$) Global minimum: $e^{-3}$ (at $x = -1$):::## Convexity### 03 Convex Function Properties {data-difficulty="2"}Consider two convex functions $f,g : \mathbb{R} \to \mathbb{R}$.1. Show that $f + g$ is convex.2. Now, assume that $g$ is additionally non-decreasing, i.e., $g(y) \geq g(x)$ for all $x \in \mathbb{R}$, for all $y \in \mathbb{R}$ with $y > x$. Show that $g \circ f$ is convex.::: {.content-visible when-profile="solution"}#### Solution {.solution-header}**Part (a): Sum of convex functions**Since $f$ and $g$ are convex, for any $x, y \in \mathbb{R}$ and $\lambda \in [0,1]$:- $f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda)f(y)$- $g(\lambda x + (1-\lambda)y) \leq \lambda g(x) + (1-\lambda)g(y)$For $h(x) = f(x) + g(x)$:$$\begin{align}h(\lambda x + (1-\lambda)y) &= f(\lambda x + (1-\lambda)y) + g(\lambda x + (1-\lambda)y) \\&\leq \lambda f(x) + (1-\lambda)f(y) + \lambda g(x) + (1-\lambda)g(y) \\&= \lambda[f(x) + g(x)] + (1-\lambda)[f(y) + g(y)]\\&= \lambda h(x) + (1-\lambda)h(y)\end{align}$$Therefore, $f + g$ is convex.**Part (b): Composition with non-decreasing function**Let $h(x) = g(f(x))$. We need to show $h$ is convex.For any $x, y \in \mathbb{R}$ and $\lambda \in [0,1]$:Since $f$ is convex:$$f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda)f(y)$$Since $g$ is non-decreasing and convex:$$g(f(\lambda x + (1-\lambda)y)) \leq g(\lambda f(x) + (1-\lambda)f(y))$$Since $g$ is convex:$$g(\lambda f(x) + (1-\lambda)f(y)) \leq \lambda g(f(x)) + (1-\lambda)g(f(y))$$Combining these inequalities:$$h(\lambda x + (1-\lambda)y) = g(f(\lambda x + (1-\lambda)y)) \leq \lambda h(x) + (1-\lambda)h(y)$$Therefore, $g \circ f$ is convex.**ML Application**: This explains why compositions like $\log(\sum_i e^{f_i(x)})$ (used in softmax) preserve convexity when the inner functions are convex.:::### 04 Testing Convexity in ML Functions {data-difficulty="2"}Determine whether the following ML-related functions are convex, concave, or neither on the given intervals:1. **Mean Squared Error**: $L(w) = \frac{1}{2}(w - 3)^2$ on $\mathbb{R}$2. **ReLU Activation**: $\text{ReLU}(x) = \max(0, x)$ on $\mathbb{R}$3. **Sigmoid Function**: $\sigma(x) = \frac{1}{1 + e^{-x}}$ on $\mathbb{R}$::: {.content-visible when-profile="solution"}#### Solution {.solution-header}1. **Mean Squared Error**: $L''(w) = 1 > 0$ for all $w$ → **Convex** on $\mathbb{R}$ This is why linear regression has a unique global minimum.2. **Logistic Loss**: $\ell'(z) = \frac{-e^{-z}}{1 + e^{-z}}$, $\ell''(z) = \frac{e^{-z}}{(1 + e^{-z})^2} > 0$ for all $z$ → **Convex** on $\mathbb{R}$ This guarantees logistic regression converges to a global optimum.3. **Negative Log-Likelihood**: $NLL'(p) = -\frac{1}{p}$, $NLL''(p) = \frac{1}{p^2} > 0$ for $p > 0$ → **Convex** on $(0, 1)$ This is why maximum likelihood estimation works well.4. **ReLU Activation**: - For $x < 0$: $\text{ReLU}(x) = 0$ (constant, so convex) - For $x > 0$: $\text{ReLU}(x) = x$ (linear, so convex) - At $x = 0$: not differentiable, but still **Convex** on $\mathbb{R}$5. **Sigmoid Function**: $\sigma''(x) = \sigma(x)(1-\sigma(x))(1-2\sigma(x))$ - $\sigma''(x) > 0$ when $\sigma(x) < \frac{1}{2}$ (i.e., $x < 0$) - $\sigma''(x) < 0$ when $\sigma(x) > \frac{1}{2}$ (i.e., $x > 0$) → **Neither** convex nor concave on $\mathbb{R}$ (S-shaped curve):::### 05 L2-Regularized Linear Regression {data-difficulty="2"}Consider the L2-regularized mean squared error loss function:$$R_\lambda(w) = \frac{1}{n}\sum_{i=1}^{n}(wx_i - y_i)^2 + \lambda w^2$$where $\{(x_i, y_i)\}_{i=1}^n$ are training data points, $w$ is the model parameter, and $\lambda > 0$ is the regularization parameter.1. Find the optimum $w^*$ and determine if it's a minimum or maximum.2. Is the function $R_\lambda(w)$ convex? Justify your answer.3. Is the minimizer unique? Explain why this is important for machine learning.::: {.content-visible when-profile="solution"}#### Solution {.solution-header}**Part 1: Finding the optimum**First, compute the derivative:$$\frac{dR_\lambda}{dw} = \frac{2}{n}\sum_{i=1}^{n}(wx_i - y_i)x_i + 2\lambda w$$$$= \frac{2w}{n}\sum_{i=1}^{n}x_i^2 - \frac{2}{n}\sum_{i=1}^{n}x_i y_i + 2\lambda w$$Setting the derivative to zero:$$w\left(\frac{1}{n}\sum_{i=1}^{n}x_i^2 + \lambda\right) = \frac{1}{n}\sum_{i=1}^{n}x_i y_i$$**Optimal solution**:$$w^* = \frac{\sum_{i=1}^{n}x_i y_i}{\sum_{i=1}^{n}x_i^2 + n\lambda}$$To determine if it's min or max, compute the second derivative:$$\frac{d^2R_\lambda}{dw^2} = \frac{2}{n}\sum_{i=1}^{n}x_i^2 + 2\lambda > 0$$Since the second derivative is positive, $w^*$ is a **minimum**.**Part 2: Convexity**The second derivative is:$$\frac{d^2R_\lambda}{dw^2} = \frac{2}{n}\sum_{i=1}^{n}x_i^2 + 2\lambda$$Since $\lambda > 0$ and $\sum_{i=1}^{n}x_i^2 \geq 0$, we have:$$\frac{d^2R_\lambda}{dw^2} \geq 2\lambda > 0$$Therefore, $R_\lambda(w)$ is **strictly convex**.**Part 3: Uniqueness**Yes, the minimizer is **unique**. This follows from strict convexity:- Since $\frac{d^2R_\lambda}{dw^2} > 0$ for all $w$, the function is strictly convex- Strictly convex functions have at most one global minimum- We found a critical point where $\frac{dR_\lambda}{dw} = 0$, so this must be the unique global minimum**Why this is important for ML**:1. **Guaranteed convergence**: Optimization algorithms will always find the same solution2. **No local minima**: Any optimization method will find the global optimum3. **Numerical stability**: Even when $\sum x_i^2$ is small (near-singular), $\lambda$ ensures stability4. **Reproducible results**: Same data always gives same model parameters**Key insight**: The regularization term $\lambda w^2$ not only prevents overfitting but also ensures the optimization problem is well-posed!:::### 06 Logistic Loss and Its Properties {data-difficulty="3"}::: {.callout-note collapse="true"}### ContextThe logistic loss is the foundation of logistic regression, one of the most important algorithms in machine learning for binary classification. Understanding its derivative is crucial for gradient-based optimization.:::Consider the logistic loss function:$$\ell(z;y) = -y\log\sigma(z) - (1-y)\log(1-\sigma(z))$$where $\sigma(z) = \frac{1}{1+e^{-z}}$ is the sigmoid function, $z$ is the logit (linear combination of features), and $y \in \{0,1\}$ is the true binary label.1. **Task**: Show that $\frac{d}{dz}\ell(z;y) = \sigma(z) - y$.2. **Bonus**: Check if the function $g(z) = (y - \sigma(z))^2$ is convex with respect to $z$.::: {.content-visible when-profile="solution"}#### Solution {.solution-header}**Part 1: Derivative of logistic loss**First, recall that $\sigma(z) = \frac{1}{1+e^{-z}}$ and $\frac{d\sigma}{dz} = \sigma(z)(1-\sigma(z))$.Let's compute the derivative term by term:$$\frac{d}{dz}\ell(z;y) = \frac{d}{dz}[-y\log\sigma(z) - (1-y)\log(1-\sigma(z))]$$For the first term:$$\frac{d}{dz}[-y\log\sigma(z)] = -y \cdot \frac{1}{\sigma(z)} \cdot \frac{d\sigma}{dz} = -y \cdot \frac{1}{\sigma(z)} \cdot \sigma(z)(1-\sigma(z)) = -y(1-\sigma(z))$$For the second term:$$\frac{d}{dz}[-(1-y)\log(1-\sigma(z))] = -(1-y) \cdot \frac{1}{1-\sigma(z)} \cdot \frac{d}{dz}[1-\sigma(z)]$$$$= -(1-y) \cdot \frac{1}{1-\sigma(z)} \cdot (-\sigma(z)(1-\sigma(z))) = (1-y)\sigma(z)$$Combining both terms:$$\frac{d}{dz}\ell(z;y) = -y(1-\sigma(z)) + (1-y)\sigma(z)$$$$= -y + y\sigma(z) + \sigma(z) - y\sigma(z) = \sigma(z) - y$$Therefore: $$\boxed{\frac{d}{dz}\ell(z;y) = \sigma(z) - y}$$**Part 2: Convexity of $(y - \sigma(z))^2$**Let $g(z) = (y - \sigma(z))^2$. To check convexity, we compute the second derivative.First derivative:$$g'(z) = 2(y - \sigma(z)) \cdot (-\sigma'(z)) = -2(y - \sigma(z))\sigma(z)(1-\sigma(z))$$Second derivative:$$g''(z) = -2\frac{d}{dz}[(y - \sigma(z))\sigma(z)(1-\sigma(z))]$$Using the product rule and chain rule:$$g''(z) = -2[(-\sigma'(z))\sigma(z)(1-\sigma(z)) + (y - \sigma(z))\frac{d}{dz}[\sigma(z)(1-\sigma(z))]]$$Since $\frac{d}{dz}[\sigma(z)(1-\sigma(z))] = \sigma'(z)(1-2\sigma(z))$ and $\sigma'(z) = \sigma(z)(1-\sigma(z))$:$$g''(z) = -2[-\sigma(z)(1-\sigma(z)) \cdot \sigma(z)(1-\sigma(z)) + (y - \sigma(z))\sigma(z)(1-\sigma(z))(1-2\sigma(z))]$$$$= 2\sigma^2(z)(1-\sigma(z))^2 - 2(y - \sigma(z))\sigma(z)(1-\sigma(z))(1-2\sigma(z))$$$$= 2\sigma(z)(1-\sigma(z))[\sigma(z)(1-\sigma(z)) - (y - \sigma(z))(1-2\sigma(z))]$$**Analysis**: The sign of $g''(z)$ depends on the bracketed term and can be positive or negative depending on the values of $y$ and $\sigma(z)$. **Conclusion**: $g(z) = (y - \sigma(z))^2$ is **not generally convex** with respect to $z$, unlike the original logistic loss $\ell(z;y)$.**ML Insight**: This is why we use the logistic loss $\ell(z;y)$ instead of the squared error $(y - \sigma(z))^2$ for binary classification - the logistic loss is convex and guarantees global optimality!:::### 07 Lipschitz Continuity & Gradient Clipping {data-difficulty="3"}::: {.callout-note collapse="true"}### Context: Lipschitz ContinuityA function $f: \mathbb{R} \to \mathbb{R}$ is called **L-Lipschitz continuous** if there exists a constant $L \geq 0$ such that:$$|f(x) - f(y)| \leq L|x - y|$$for all $x, y$ in the domain. The smallest such constant $L$ is called the **Lipschitz constant**.This property is crucial in deep learning for gradient clipping, ensuring gradients don't explode during training.:::Consider the sigmoid function $\sigma(z) = \frac{1}{1+e^{-z}}$.**Task**: Prove that $\sigma(z)$ is L-Lipschitz continuous and find the **optimal** (smallest possible) Lipschitz constant $L$.::: {.content-visible when-profile="solution"}#### Solution {.solution-header}To find the Lipschitz constant, we need to find the supremum of $|\sigma'(z)|$ over all $z \in \mathbb{R}$.**Step 1: Compute the derivative**$$\sigma'(z) = \frac{d}{dz}\left(\frac{1}{1+e^{-z}}\right) = \frac{e^{-z}}{(1+e^{-z})^2} = \sigma(z)(1-\sigma(z))$$**Step 2: Find the maximum of $|\sigma'(z)|$**Since $\sigma(z) \in (0,1)$ for all $z$, we have $\sigma'(z) > 0$, so $|\sigma'(z)| = \sigma'(z) = \sigma(z)(1-\sigma(z))$.To find the maximum, we differentiate:$$\frac{d}{dz}[\sigma(z)(1-\sigma(z))] = \sigma'(z)(1-\sigma(z)) + \sigma(z)(-\sigma'(z))$$$$= \sigma'(z)(1-2\sigma(z)) = \sigma(z)(1-\sigma(z))(1-2\sigma(z))$$Setting this to zero: $1-2\sigma(z) = 0$, which gives $\sigma(z) = \frac{1}{2}$.This occurs when $z = 0$ (since $\sigma(0) = \frac{1}{2}$).**Step 3: Evaluate at the critical point**$$\sigma'(0) = \sigma(0)(1-\sigma(0)) = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$$**Step 4: Check the behavior at infinity**- As $z \to +\infty$: $\sigma(z) \to 1$, so $\sigma'(z) \to 0$- As $z \to -\infty$: $\sigma(z) \to 0$, so $\sigma'(z) \to 0$**Conclusion**: $$\max_{z \in \mathbb{R}} |\sigma'(z)| = \frac{1}{4}$$Therefore, $\sigma(z)$ is $\frac{1}{4}$-Lipschitz continuous, and $L = \frac{1}{4}$ is the **optimal** Lipschitz constant.**Verification**: For any $x, y \in \mathbb{R}$:$$|\sigma(x) - \sigma(y)| = |\sigma'(c)||x - y| \leq \frac{1}{4}|x - y|$$where $c$ is between $x$ and $y$ (by the Mean Value Theorem).**ML Implications**:1. **Gradient Clipping**: Since $|\sigma'(z)| \leq \frac{1}{4}$, the sigmoid activation naturally bounds gradients, preventing gradient explosion during backpropagation.2. **Stable Training**: The Lipschitz property ensures that small changes in input lead to small changes in output, providing numerical stability.3. **Vanishing Gradients**: However, when $\sigma(z)$ is near 0 or 1 (saturated regions), $\sigma'(z) \approx 0$, leading to vanishing gradient problems in deep networks.4. **Architecture Design**: This analysis explains why modern architectures often use ReLU-family activations instead of sigmoids for hidden layers, as ReLU doesn't suffer from gradient saturation.5. **Optimization Theory**: Lipschitz continuity is essential for convergence guarantees in gradient-based optimization algorithms.:::## Taylor Series### 08 Taylor Series Expansions {data-difficulty="2"}Find the Taylor series expansion around the given point for each function:1. $f(x) = e^x$ around $x = 0$ (Maclaurin series)2. $g(x) = \ln(x)$ around $x = 1$3. $h(x) = \cos(x)$ around $x = 0$ (first 4 non-zero terms)::: {.content-visible when-profile="solution"}#### Solution {.solution-header}1. $e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots$2. $\ln(x) = \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n}(x-1)^n = (x-1) - \frac{(x-1)^2}{2} + \frac{(x-1)^3}{3} - \frac{(x-1)^4}{4} + \cdots$3. $\cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots$:::# 🛠️ Գործնական ToDo- [🛠️📺 Գործնականի տեսագրությունը]()- [🛠️🗂️ Գործնականի PDF-ը]()# 🎲 41 (05)- ▶️[Кот в сапогах 2: Последнее желание (լուրջ եմ ասում, շատ լավն ա :-))](https://new.kinogo.fm/507-kot-v-sapogah-2-poslednee-zhelanie-2022.html)- 🔗[Random link](https://youtube.com/shorts/Z_Gnf2PA56w?si=RRakgWnV1IweJzgC)- 🇦🇲🎶[Տիգրան Մանսուրյան (Հին Օրերի Երգը)](https://www.youtube.com/watch?v=f2UE7tJLsns)- 🌐🎶[Elliot Smith (Between the Bars)](https://www.youtube.com/watch?v=9pPAFLnO8zs)- 🤌[Կարգին ToDo]()<a href="http://s01.flagcounter.com/more/1oO"><img src="https://s01.flagcounter.com/count2/1oO/bg_FFFFFF/txt_000000/border_CCCCCC/columns_2/maxflags_10/viewers_0/labels_0/pageviews_1/flags_0/percent_0/" alt="Flag Counter"></a>